Note Quantization

At PyCon last year I talked about my project Czerny which I announced four years ago but haven't really worked on much since.

The idea of Czerny was to align representations of performances with representations of score (particularly with Piano music) to both (a) assess errors; (b) study articulation, timing variations, etc.

Last week Adrian Holovaty asked me (in response to a comment about me still wanting to write a guide to music theory for programmers—not sure if Adrian knows about Czerny) about algorithms for note quantization.

As it's of interest to me and somewhat related to Czerny, I decided I'd put down some thoughts.

Now I'm sure there's academic literature on this but before I dive into that, I wanted to give some it in-depth thought of my own. This thought stream is my initial place for notes (no pun intended).

In Czerny, I largely side-stepped the issue of quantization between the alignment of notes that I do doesn't even look at note start times, only note order (at least for now).

Plus with Czerny, I assume there's a representation of the score, whereas the problem of note quantization generally assumes there's no reference score (and I'll make that assumption in what follows).

I should note that, while quantization is often associated with fixing mistakes in performances, that is neither my interest, nor I suspect Adrian's.

Rather I'm interested in taking a representation of a performance and non-destructively calculating a quantized version to both answer questions about this quantized version (e.g. tempo and tempo changes) and also analyze style (in much the same way as Czerny is intended to help with, albeit in the presence of a score in the Czerny case).

One of the fundamental aspects of music theory is that we deal not in frequencies and clock timings but more abstractly in pitches (or scale degrees) and rhythms set against a grid.

In the case of pitch, we go from frequency to letter name + octave via a choice of tuning and temperament, then abstract away the octave and factor out the key to get an abstraction like "the 3rd note of the scale" or a "IV⁶₄ chord" or whatever.

In the case of durations and rhythms (which is our focus in this stream) we go from offsets (say in seconds) to measures and beats.

Even though the main point of quantization is dealing with notes that aren't "exactly on the grid" there are still some preliminary issues we need to deal with even in the case where a performance is exactly aligned with the grid.

First, let's define what I mean by a "performance".

By performance I mean a set of events that include at least a time offset.

Typically events will also include pitch information and possibly other things such as velocity (in the case of a MIDI performance) but none of these will enter into our discussion.

I'm deliberately avoiding duration initially because I want to pursue placing notes on the grid (and, indeed inferring the grid to start with) before any discussion about note duration.

Note duration is hugely important to a lot of applications (not least of which the kind of analysis of articulation I want in Czerny) but I think we can proceed a long way before considering them.

It's also possible that velocity will have role to play in identify the time signature but again, we can defer that possibility for a while.

Let's started with the simplest possible case: a series of events with uniform rhythm, aligned perfectly with the grid, with uniform tempo, no anacrusis / pick up, and with the time offset of the first note equal to zero.

This may seem ridiculously simple (and almost useless) but it will allow us to define some terms and set things up.

We can then successively remove each of these simplifications.

There are two other assumptions we're going to make initially.

Firstly, we're going to assume common time: four simple beats to a measure.

Secondly, we're going to assume that our tempo lies between 70 bpm and 140 bpm. In other words, a performance at 150 bpm will be interpreted at 75 bpm with note lengths half of what they would be viewed as under 150 bpm.

Given the case outlined above, the performance might look something like this (remember we're only considering the time offset of each event):

0s, 0.5s, 1.0s, 1.5s, 2.0s, ...

Given the constraints we initially specified above, this can only be a series of quarter-notes at 120 bpm.

So our archetypal relationship between the "beat grid" and time offsets is:

t = nτ

where t is the time offset, n is the beat number and τ is the tempo.

Now, of course, we really want to relate the time offset with an event number so we need a mapping of event number to beat number. Let's use b_i to denote the beat number of the i-th note.

We then have

t_i = b_iτ

We can quickly accommodate pick ups and a silence before the first event as follows:

• let T be the time offset of the start of the first full measure
• allow negative b_i for pick ups / anacrusis

Only the first affects our equation, which becomes:

t_i = b_iτ + T

To given an example, if there's a one beat pickup, b₁would equal -1.

To be clear: we're not doing quantization yet, we're just building a model. Once we have a model, it will be a lot easier to discuss how the parameters of that model might be inferred from a performance.

Now let's remove the assumption that the tempo is the same throughout the piece. We'll start with handling sections of different tempi, then discuss ritardando. We'll delay discussion of rubato for the moment.

Say a piece begins at one tempo, τ₁ and then changes to τ₂ instantaneously.

We'll model this as two sections, each with it's own equation:

t_1i = b_1iτ₁ + T₁

t_2j = b_2jτ₂ + T₂

Here t_1i means the time-offset of the i-th note in section one. b_1i maps notes in section one to beat numbers. T₁ tells us the time offset of the start of the first full bar in the first section.

And the same for the second section, replacing 1 with 2. In the above, I've also used j instead of i to make more explicit that it ranges over a different set of numbers (although I will not always do that).

Note that T₂ is basically the total length of the first section plus the pause between the sections if any.

If we model the tempo of different sections in this way, why not then model each measure this way?

This would allow for all sorts of variation within a measure without affecting the tempo at the measure-level grid.

The same applies to notes within the beat-level of the grid.

So let's develop our model further to support hierarchy.

We'll initially focus purely on the time-offset of various points on a multi-level grid before adding the mapping of notes to that grid.

Although we'll sometimes have grid levels above the measure (as we saw earlier with sections at different tempi), let's imagine for now that the top level is the measure level.

Let's then say that the time-offset of the m-th measure is T_m.

Let's then introduce a grid level directly below the measure but above the beat. I'll call this the beat group. The idea here is that the 4 beats of a 4/4 measure can be thought of as two groups of two. Similarly, something like 5/8 can be thought of as a two-beat group followed by a three-beat group or vice versa.

We'll say that the time-offset of the g-th beat group of the m-th measure from the start of the measure is T_mg.

Hence the the absolute time offset of the g-th beat group of the m-th measure would be T_m + T_mg.

I'm undecided when to use t vs T at the moment (perhaps one should be absolute and the other relative to start of the previous level of the hierarchy; we'll come back to all this)

The b-th beat of the g-th beat group of the m-th measure, would unsurprisingly be T_mgb in this model.

We'll call the level below the beat, the sub-beat and it's offset from the beat will be T_mgbs where s is the sub-beat number within the beat.

It is worth noting that the difference between 3/4 and 6/8 in this model is that a 3/4 measure consists of 3 beats each made up of 2 sub-beats and a 6/8 measure consists of 2 beats each made up of 3 sub-beats.

Hence simple vs compound time is distinguished by 2 or 3 sub-beats per beat.

Note that the notion of a beat group is degenerate in this case and is only useful in cases were the number of beats per measure is more than three.

One hypothesis is that from measure on down, each hierarchy either splits into 2 or 3. Open questions are how tuplets are to be modeled and also whether something like 13/8 would need multiple levels of beat group.

But I don't think we're relying on that hypothesis here anyway.

Let's, denote the number of beat groups in measure m by G_m, the number of beats in beat group g of measure m by B_mg and the number of sub-beats in beat b or beat group g of measure m by S_mgb.

If the number of beat groups in a measure is the same regardless of measure, we'll write either G_* or just G. Similarly, we can say things like B_*g if B varies by beat group but not measure.

We'll similarly use this * notation with T if possible.

Let's go back to our simple 120 bpm quarter notes in 4/4.

We have:

G = 2

B = 2

τ = 2.0 (120 bpm 4/4 = 2 seconds per measure)

and:

T_m = τ(m - 1)

T_*g = (τ / G)(g - 1)

T_**b = (τ / (GB))(b - 1)

The previous equations set up a uniform grid, but there's no reason not to make τ dependent on m, mg, mgb, and mgbs.

So we end up with something like:

T_m = τ_m(m - 1)

T_mg = τ_mg(g - 1)

T_mgb = τ_mgb(b - 1)

T_mgbs = τ_mgbs(s - 1)

Note that we don't need to divide by G or B as before because that's baked into τ_mg and τ_mgb respectively.

In our constant tempo version,

τ_m = τ

τ_mg = τ / G

and so on.

If we do use a different notation (perhaps t vs T) for absolute time-offset versus time-offset from the most recent tick of the grid-level above, then note that, in the above, the measure-level would be notated differently to the lower-levels.

If we introduced grid-levels above the measure (phrase, theme, theme group, section, movement, etc) then the measure-level would become relative.

In fact, let's put a stake in the ground a decide from this point that t means relative time-offset and T means absolute time-offset.

This, of course, makes many of the equations earlier now incorrect (or inconsistent with this new notation).

I'll go through and restate some of the major ideas with the new notation (rather than edit earlier thoughts and lose the progression of ideas).

Let's then say that the time-offset of the m-th measure is T_m.

This remains true.

We'll say that the time-offset of the g-th beat group of the m-th measure from the start of the measure is T_mg.

Hence the the (sic) absolute time offset of the g-th beat group of the m-th measure would be T_m + T_mg.

We'll now say that the time-offset of the g-th beat group of the m-th measure from the start of the measure is t_mg.

Hence the absolute time offset of the g-th beat group of the m-th measure would be T_mg = T_m + t_mg.

The b-th beat of the g-th beat group of the m-th measure, would unsurprisingly be T_mgb in this model.

It's ambiguous if I'm talking about absolute or relative here but it's T_mgb or t_mgb respectively.

We'll call the level below the beat, the sub-beat and it's offset from the beat will be T_mgbs where s is the sub-beat number within the beat.

The sub-beat's offset from the beat will be t_mgbs where s is the sub-beat number within the beat.

Let's, denote the number of beat groups in measure m by G_m, the number of beats in beat group g of measure m by B_mg and the number of sub-beats in beat b or beat group g of measure m by S_mgb.

If the number of beat groups in a measure is the same regardless of measure, we'll write either G_* or just G. Similarly, we can say things like B_*g if B varies by beat group but not measure.

We'll similarly use this * notation with T if possible.

All still true but we'll also use the * notation with t as well.

Our general equations:

T_m = τ_m(m - 1)

T_mg = τ_mg(g - 1)

T_mgb = τ_mgb(b - 1)

T_mgbs = τ_mgbs(s - 1)

become

t_m = τ_m(m - 1)

t_mg = τ_mg(g - 1)

t_mgb = τ_mgb(b - 1)

t_mgbs = τ_mgbs(s - 1)

But we can now also add:

T_mg = T_m + t_mg = T_m + τ_mg(g - 1)

T_mgb = T_mg+ t_mgb = T_mg+ τ_mgb(b - 1)

T_mgbs = T_mgb + t_mgbs = T_mgb + τ_mgbs(s - 1)

Or alternatively:

T_mgbs = T_m + τ_mg(g - 1) + τ_mgb(b - 1) + τ_mgbs(s - 1)

I just had a horrible, thought...

Consider something like:

t_mgb = τ_mgb(b - 1)

We're not properly considering the length of earlier beats in a beat group in determining the offset of later beats. Consider G=1, B=3 (which I've suggested above would be 3/4 time).

t_m11 = 0

t_m12 = τ_m11

t_m13 = τ_m11 + τ_m12

So obviously, if τ_m1* are constant then,

t_m1b = τ_m1*(b - 1)

as before but if not constant we really need to take the sum.

Perhaps ThoughtStreams needs MathJax support so I can do this properly :-)

In the meantime, here's a diagram outlining where we're currently at:

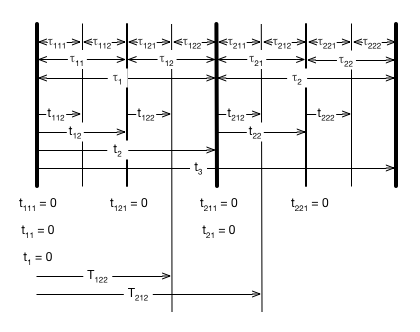
Just as reminder that we're still just talking about the "grid". Actual notes may fall slightly off the grid but our goal (eventually) is to model the grid such that the deltas between note placement and the grid are minimized.

Swing can be modeled by shifting just the even sub-beats. The following shows a single 4/4 measure without and with swing.

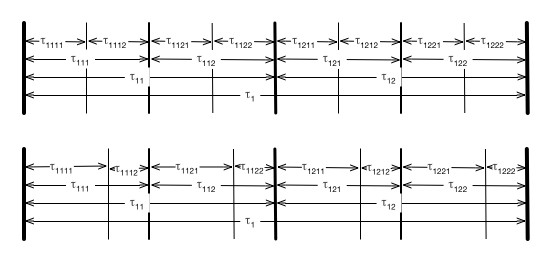
Notice this can be modeled just as

τ_mgbs = 1/2 τ_mgb

for no swing and something like:

τ_mgb1 = 2/3 τ_mgb

τ_mgb2 = 1/3 τ_mgb

for swing. Of course, swinging doesn't have to be 2/3, but we can easily model other fractions in similar manner.

What's particularly compelling about the above model for swing is that, as long as actual note placement is relative to the grid, we can easily swing a straight time rhythm or de-swing a swing rhythm back to a straight time just by changing the grid parameters τ_mgb1 and τ_mgb2.

I'm wondering now about the redundancy in the fact that

τ_mgb1 + τ_mgb2 = τ_mgb

assuming S_mgb = 2.

Related is the fact that any t ending in 1 (e.g. t₁, t_m1, t_mg1, t_mgb1) is always 0.

There is another issue I need to address before finally getting to questions of how to actually infer a grid from a performance.

Imagine that we have a ritardando across two measures, m and m+1 such that T_m = 100, T_m+1 = 102, T_m+2 = 104. In other words τ_m = 2 and τ_m+1 = 4.

The tempo doesn't suddenly halve between measure m and measure m+1. We need to work out a decent model that adjusts each beat-group, beat and sub-beat τ appropriately for a continuous change in tempo.