Via the science fiction author Greg Egan I've found out about the wonderful fractals discovered by Dan Christensen and Sam Derbyshire based on the Littlewood polynomials.
A Littlewood polynomial is one where the coefficients are all either -1 or 1.
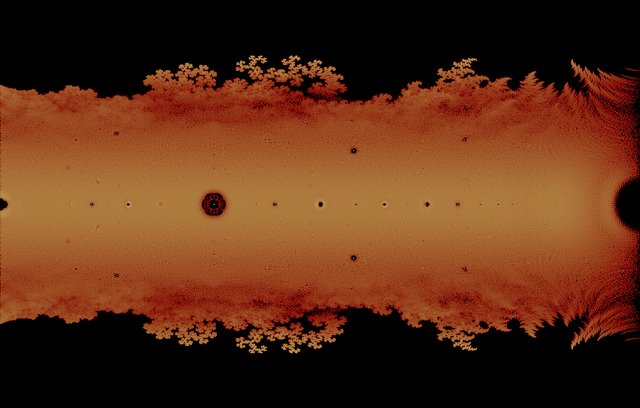
If you take all the complex roots of an n-th degree Littlewood polynomial and plot them on the complex plane you get a wonderful fractal.

The above is an 18th-degree Littlewood fractal I generated using some Python code I'll soon put up on Github.
With itertools.product it's easy to generate all the Littlewood coefficients:
for coefficients in product(*([[-1, 1]] * DEGREE)):
and then with numpy.roots it's easy to generate all the roots for that polynomial:
for root in roots((1,) + coefficients):
My current approach to visualization is to take the number of roots in the region represented by a pixel and take the ratio of the log of that number to the log of the maximum number of roots any pixel has:
value_at_pixel = log(num_roots_at_pixel) / log(max_roots)
I then generate an RGB value from an HSV of
(value_at_pixel / 4, 1 - value_at_pixel, 0.5 + value_at_pixel)
with colorsys.hsv_to_rgb.
Given that it looks like a cross between the One Ring and the Eye of Sauron perhaps the fractal should have a Tolkien-inspired name :-)
A close up of a dragon-curve-like fractal from the inside bottom right:

I wonder if I could speed up the PNG generation by memoizing the HSV to RGB (or more specifically, the root count to RGB) code.
Caching root count to RGB helps a fair amount (around 25% time reduction on my initial tests)
Running with pypy would speed things up, but numpypy doesn't support roots from what I can tell.
The root generation and the heatmap generation can be split into two completely separate processes so I'm working on that now.
This means the roots could be calculated once for a particular degree without having to do it over and over again for different image resolutions.
Dan Christensen, in a comment on John Baez's blog post about the Littlewood fractals says:
Using python and scipy, and carefully taking into account the 8-fold symmetry, I can generate the degree 24 roots in about 3 hours, and plot them in about 10 minutes. I store about 55 million roots (again using symmetry).
As a point of comparison, my root generation for degree 24 on my iMac a year later is currently just under 2 hours.
I'm taking advantage of 4-fold symmetry as I wasn't aware of an additional symmetry but I've just plotted the top quadrant using polar coordinates and now it's obvious:
So in root generation not only need I only consider Re(z) >=0 and Im(z) >=0 but also |z| <= 1.
The Beauty of Roots by John Baez, Dan Christensen, Sam Derbyshire and Greg Egan: easy version / hard version
Pushed separate root-generation and heatmap-rendering code (including polar version) to Github.
Run roots.py then heatmap.py.